
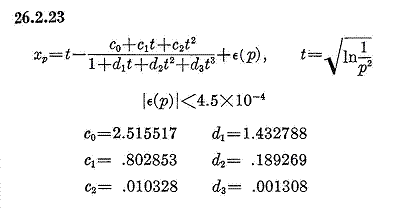
The Pareto distribution is mathematically an exponential-gamma mixture. For example, the gamma distribution is derived from the gamma function. The above table categorizes the distributions according to how they are mathematically derived.
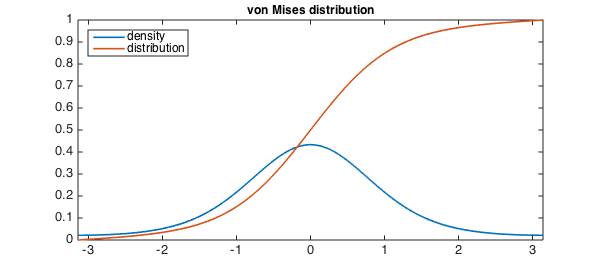
Click on the links to find out more about the distributions. Others are obtained by mixing distributions. Other distributions are obtained by raising a distribution to a power. These are distributions that are gamma distributions with certain restrictions on the one or both of the gamma parameters.
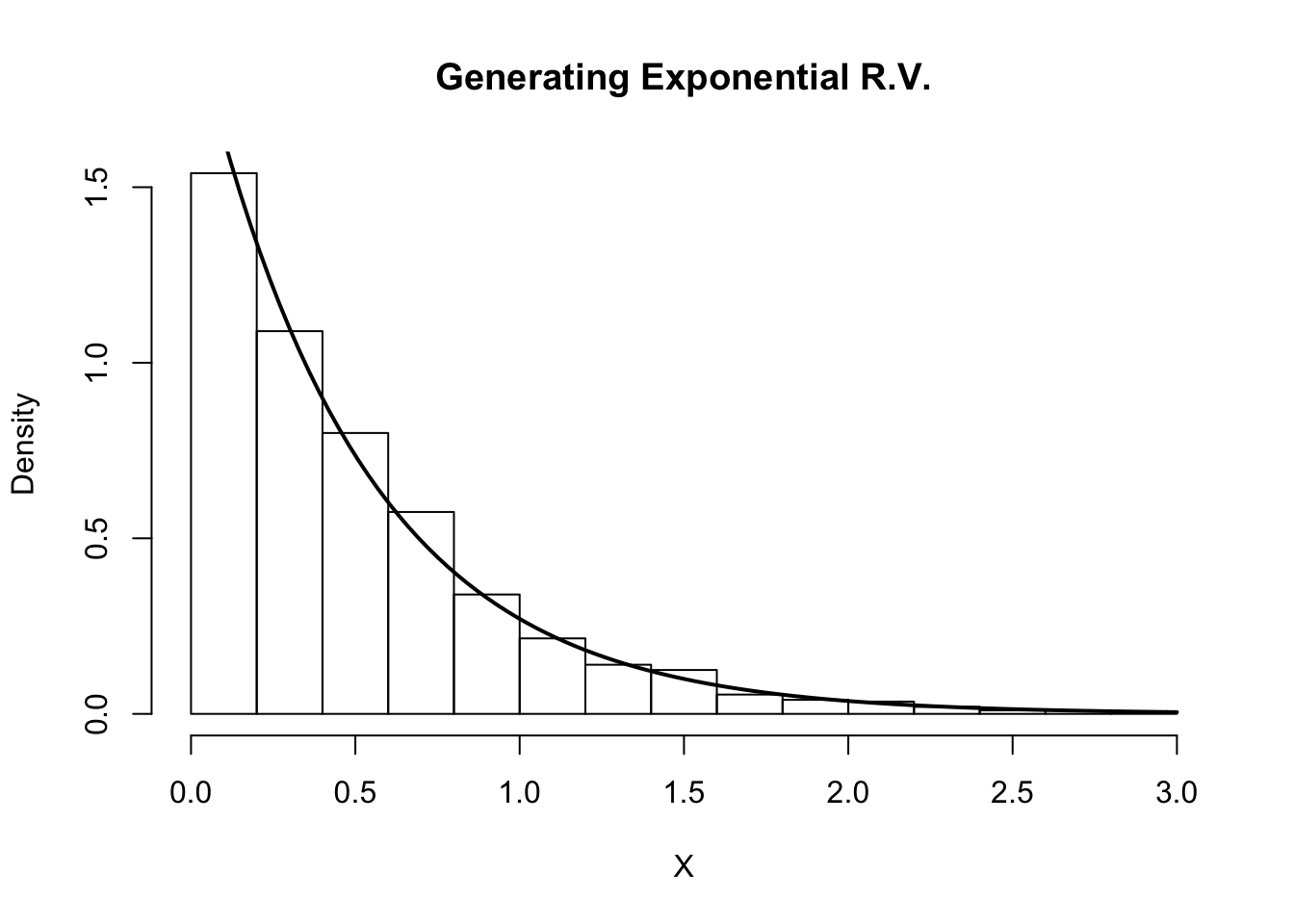
The gamma sub family includes the exponential distribution, Erlang distribution and chi-squared distribution. Mathematically, the gamma distribution is a two-parameter continuous distribution defined using the gamma function. So the catalog starts with the gamma distribution at the top and then branches out to the other related models. Many of the models highlighted here are related to gamma distribution either directly or indirectly. This post also serves a navigation device (the table shown below contains links to the blog posts). However, the list is a good place to begin. There are other models that are also suitable for actuarial applications but not accounted for here. The list presented here is not exhaustive it is only a brief catalog. They are all potential candidates for models of severity in insurance applications and in other actuarial applications. The number of parameters in these models ranges from one to two, and in a small number of cases three. Various parametric continuous probability models have been presented and discussed in this blog.


 0 kommentar(er)
0 kommentar(er)
